网络结构
单向循环神经网络
循环神经网络(Recurrent Neural Network, RNN)是一类以序列(sequence)数据为输入,在序列的演进方向进行递归且所有节点(循环单元)按链式连接的递归神经网络。基本的循环神经网络如下图左侧所示:
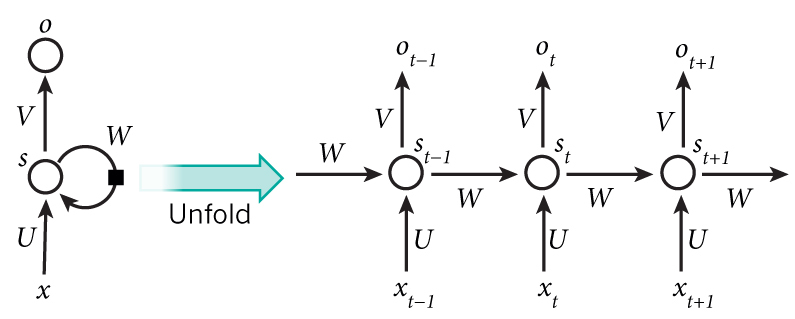
图中右侧是左侧的横向展开。这个神经网络由输入层、一个隐藏层和一个输出层组成,但是在隐藏层上,神经元的加权输入不仅取决于它与上一层连接的权重矩阵,还取决于它前一时刻的加权输入和一个特殊的矩阵 W。即结果可以使用下式来表示:
$$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t)\\ \mathrm{s}_t&=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})\\ \end{aligned}$$两式合并有:
$$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t)\\ &=Vf(U\mathrm{x}_t+W\mathrm{s}_{t-1}) \end{aligned}$$我们可以发现,这是一个递归式,其 $s_{t-1}$ 项与 $s_{t-2}$ 项相关联,最终会抵达序列开始的 $s_{1}$。因此这个神经网络与其他神经网络相比,有将前向序列相关联的能力。
双向循环神经网络
这里将单向循环神经网络进一步扩展,考虑向后传播有:
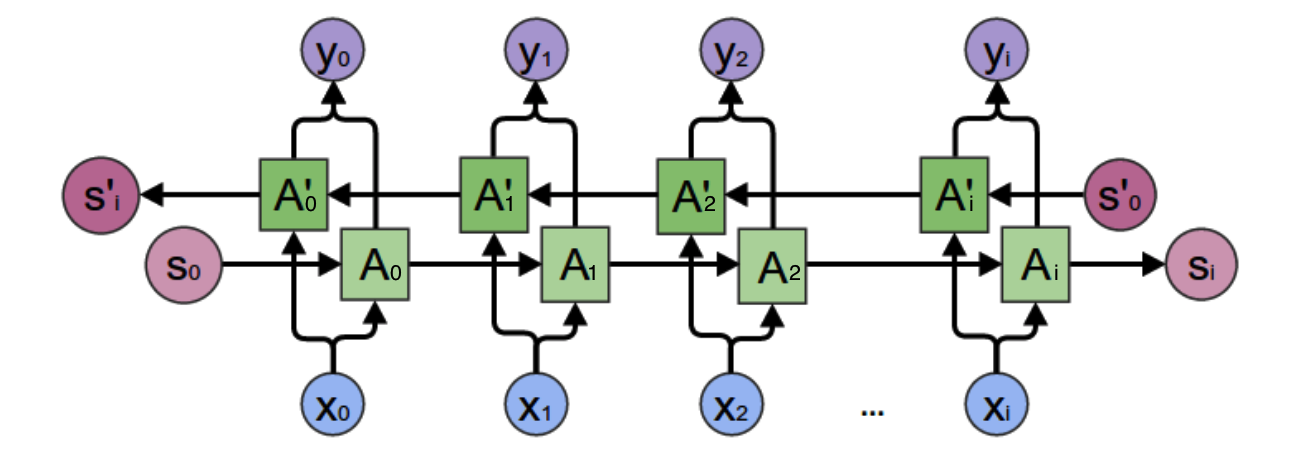
可以看出,原来单向的递归变成了双向,即一方面从序列开始进行递归,一方面从序列末端进行递归。因此计算也会稍加变化:
$$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t+V'\mathrm{s}_t')\\ \mathrm{s}_t&=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})\\ \mathrm{s}_t'&=f(U'\mathrm{x}_t+W'\mathrm{s}_{t+1}')\\ \end{aligned}$$训练算法
BPTT 算法是针对循环层的训练算法,包含下列步骤:
- 前向计算每个神经元的输出值,即$y_0$;
- 反向计算每个神经元的误差项值,即$\delta$;
- 计算每个权重的梯度,并用随机梯度下降算法更新权重。
时间误差项
对于总长度为 $t$ 的序列,任意时刻 k 的误差项 $\delta_k$ 有:
$$\begin{aligned} \delta_k^T=&\frac{\partial{E}}{\partial{\mathrm{net}_k}}\\ =&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_k}}\\ =&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{\mathrm{net}_{t-2}}}...\frac{\partial{\mathrm{net}_{k+1}}}{\partial{\mathrm{net}_{k}}}\\ \end{aligned}$$定义
$$\begin{aligned} \mathrm{net}_t&=U\mathrm{x}_t+W\mathrm{s}_{t-1}\\ \mathrm{s}_{t-1}&=f(\mathrm{net}_{t-1})\\ \end{aligned}$$则 $\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}$ 有:
$$\begin{aligned} \frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}&=\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}\\ &=W\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}} \end{aligned}$$对于 $\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}$:
$$\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}= \begin{bmatrix} f'(net_1^{t-1}) & 0 & ... & 0\\ 0 & f'(net_2^{t-1}) & ... & 0\\ &.\\&.\\ 0 & 0 & ... & f'(net_n^{t-1})\\ \end{bmatrix} =diag[f'(\mathrm{net}_{t-1})]$$即为 $f'(\mathrm{net}_{t-1}$ 构成的对角矩阵。由此:
$$\begin{aligned} \delta_k^T&=\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{\mathrm{net}_{t-2}}}...\frac{\partial{\mathrm{net}_{k+1}}}{\partial{\mathrm{net}_{k}}}\\ &=\delta_t^T \cdot Wdiag[f'(\mathrm{net}_{t-1})]\cdot Wdiag[f'(\mathrm{net}_{t-2})]...Wdiag[f'(\mathrm{net}_{k})]\\ &=\delta_t^T\prod_{i=k}^{t-1}Wdiag[f'(\mathrm{net}_{i})] \end{aligned}$$层误差项
由于:
$$\begin{aligned} \mathrm{net}_t^l&=U\mathrm{a}_t^{l-1}+W\mathrm{s}_{t-1}\\ \mathrm{a}_t^{l-1}&=f^{l-1}(\mathrm{net}_t^{l-1}) \end{aligned}$$那么:
$$\begin{aligned} (\delta_t^{l-1})^T=&\frac{\partial{E}}{\partial{\mathrm{net}_t^{l-1}}}\\ &=\frac{\partial{E}}{\partial{\mathrm{net}_t^l}}\frac{\partial{\mathrm{net}_t^l}}{\partial{\mathrm{net}_t^{l-1}}}\\ &=\frac{\partial{E}}{\partial{\mathrm{net}_t^l}}\frac{\partial{\mathrm{net}^l}}{\partial{\mathrm{a}_t^{l-1}}}\frac{\partial{\mathrm{a}_t^{l-1}}}{\partial{\mathrm{net}_t^{l-1}}} \\ &=(\delta_t^l)^TUdiag[f'^{l-1}(\mathrm{net}_t^{l-1})] \end{aligned}$$梯度计算
对于 W,有:
$$\begin{aligned} \nabla_WE=&\frac{\partial{E}}{\partial{W}}\\ &=\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{W}}\\ &=\delta_t^T\frac{\partial{W}}{\partial{W}}f(\mathrm{net}_{t-1})+ \delta_t^T\frac{\partial{f(\mathrm{net}_{t-1})}}{\partial{W}}W\\ \end{aligned}$$对于 $\frac{\partial{W}}{\partial{W}}f(\mathrm{net}_{t-1})$,有(中间省略了一些运算):
$$\begin{aligned} \delta_t^T\frac{\partial{W}}{\partial{W}}f({\mathrm{net}_{t-1}})=\begin{bmatrix} \delta_1^ts_1^{t-1} & \delta_1^ts_2^{t-1} & ... & \delta_1^ts_n^{t-1}\\ \delta_2^ts_1^{t-1} & \delta_2^ts_2^{t-1} & ... & \delta_2^ts_n^{t-1}\\ .\\.\\ \delta_n^ts_1^{t-1} & \delta_n^ts_2^{t-1} & ... & \delta_n^ts_n^{t-1}\\ \end{bmatrix}=\nabla_{Wt}E \end{aligned}$$对于 $\delta_t^T\frac{\partial{f(\mathrm{net}_{t-1})}}{\partial{W}}W$ 有:
$$\begin{aligned} \delta_t^TW\frac{\partial{f(\mathrm{net}_{t-1})}}{\partial{W}}=& \delta_t^TW\frac{\partial{f(\mathrm{net}_{t-1})}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{W}}\\ =&\delta_t^T\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{W}}\\ =&\delta_{t-1}^T\frac{\partial{\mathrm{net}_{t-1}}}{\partial{W}}\\ \end{aligned}$$那么 W 梯度有:
$$\begin{aligned} \nabla_WE=&\frac{\partial{E}}{\partial{W}}\\ =&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{W}}\\ =&\nabla_{Wt}E+\delta_{t-1}^T\frac{\partial{\mathrm{net}_{t-1}}}{\partial{W}}\\ =&\nabla_{Wt}E+\nabla_{Wt-1}E+\delta_{t-2}^T\frac{\partial{\mathrm{net}_{t-2}}}{\partial{W}}\\ =&\nabla_{Wt}E+\nabla_{Wt-1}E+...+\nabla_{W1}E\\ =&\sum_{k=1}^t\nabla_{Wk}E \end{aligned}$$同理 U 梯度有:
$$\nabla_UE=\sum_{i=1}^t\nabla_{U_i}E$$
Softmax 层与交叉熵误差
我们在前面的的神经网络中大多采用均方差误差 (MSE) 与标准输出层,这样是最简单,最方便的输出层架构方法。而在一个相关序列中,我们更常用的是使用 softmax 层作为输出层,使用交叉熵误差来确定误差大小。Softmax 函数为:
$$g(z_i)=\frac{e^{z_i}}{\sum_{k}e^{z_k}}$$
而交叉熵误差为:
$$L(y,o)=-\frac{1}{N}\sum_{n\in{N}}{y_nln\quad o_n}$$
上式中,N 是训练样本的个数,$y_n$是样本的标记,$o_n$是网络的输出。