感知器的结构及实现

基本概念

感知器（Perceptron）是 Frank Rosenblatt 发明的一种人工神经网络，其是生物神经细胞的简单抽象。

大概长下面这样：

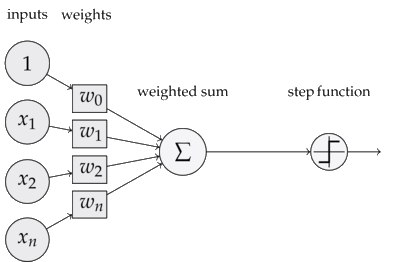
运作机理：左侧为输入层，将测试组在该处输入。经过训练过的权重加权以后得到输出结果，最后使用激活函数对结果进行判断并在输出层输出。

感知器通常包含以下内容：

• 激活函数 感知器使用特征向量来表示的前馈神经网络作为激活函数（前馈神经网络：参数仅由输入层向输出层单向传播的网络），此处使用了阶跃函数：

$$ f(x) = \begin{cases}1 & \text{if }w \cdot x + b > 0\\ 0 & \text{else}\end{cases} $$

• 输入权值：一个感知器可以接收多个输入 $x_1, x_2, x_3…x_r$，每个输入上有一个权值 $w_i$，表示权重的向量

• 偏置项$b$，偏置项即为输入为$1$时经过权重计算产生的输入值，可以认为是激活函数的偏移量。

• 输出 感知器的输出由以下函数确定：

$$ f = w \cdot x + b $$

感知器的训练

在预先确定输入向量和输出向量的正确结果以后，就可以作为训练集合对感知器进行训练，以得到合理的偏置项和贡献权值（这里假定偏置项为输入为 1 时的输出向量）。感知器的学习通过对所有训练实例进行多次的迭代进行更新的方式来建模，令 $D_m = {(x_1,y_1),\dots,(x_m,y_m)}$ 表示一个有 $$m$$ 个训练实例的训练集，每次迭代权重向量对于 $D_m$ 中的每个 $(x,y)$ 对，有：

$$w(j):= w(j) + {\alpha(y-f(x))}{x(j)}$$

而对于偏置量则为：

$$bias:= bias + {\alpha(y-f(x))}$$

其中 $\alpha$ 的意义为训练速度，通过改变 $\alpha$ 可以改变训练时权重变化的幅度，从而控制训练速度。需要注意的是，这种学习的成功与否取决于训练集自身的特征，因此存在感知器无法收敛而不能得解的可能。

感知器的实现

大小比较

import numpy as np


class Perceptron:
    def __init__(self, activator):
        self.weight = np.zeros([2])
        self.bias = 0.0
        self.activator = activator

    def predict(self, vec):
        return self.activator(np.sum(vec * self.weight) + self.bias)

    def train(self, rnd=10, rate=0.1):
        train_set = np.random.random_sample(100) * 50
        for i in range(rnd):
            print('%s, %s' % (self.weight, self.bias))
            for j in range(train_set.shape[0]):
                train = np.array([np.random.choice(train_set) for _ in range(2)])
                delta = (train[0] > train[1]) - self.predict(train)
                self.weight = list(map(lambda x: x[1] + rate * delta * x[0], zip(train, self.weight)))
                self.bias += rate * delta


def main():
    print('\nTrain:')
    p = Perceptron(lambda x: 1 if x > 0 else 0)
    p.train()

    print('\nTest:')
    test_set = np.random.random_sample(100) * 50
    for j in range(15):
        test = np.array([np.random.choice(test_set) for _ in range(2)])
        print('%s, %s' % (test, p.predict(test) == 1))
    pass


if __name__ == "__main__":
    try:
        main()
    except KeyboardInterrupt:
        pass