基本概念
由于感知器(Perceptron)的激活函数为阶跃函数,这意味着大多数时候感知器只能承担二分类之类的操作。如果数据集本身并不能(或者较难)被二分,或者说数据集不是线性可分的时候,感知器的训练就难以得到可用的权重和 bias,这时候可以考虑使用线性函数对数据进行分析。所谓使用线性函数进行分析,其实换一个说法就是线性回归啦(w)流程大概长下面这样:
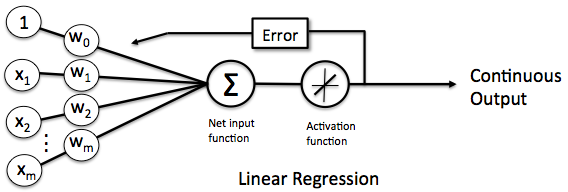
其激活函数为:
$$f(x) = x$$
其他结构与感知器相同。因此我们可以发现,其实这个网络的输出结果就是一系列参数的线性拟合:
$$\begin{aligned} y = h(x) & = w \cdot x + b \\ & = w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 + b \end{aligned}$$我们可以令$w_0 = b$, 那么原式就变成:
$$\begin{aligned} y & = w_0 \cdot x_0 + w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 \\ & = h(x) = \mathrm{w}^T\mathrm{x} \end{aligned}$$ 其中第二个式子是以向量的形式表示的。由于我们要解决的是一个回归问题,所以需要引入一个确定偏差的量,这个量也称为损失函数。一般可以使用 1/2 方差来表征误差的大小,即为下式:
$$ \nabla{E}(\mathrm{w})=\frac{1}{2}(\mathrm{y}-\bar{\mathrm{y}})^2 $$
对所有样本求和以后为:
$$\begin{aligned} E&=e^{(1)}+e^{(2)}+e^{(3)}+...+e^{(n)}\\ &=\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-\bar{y}^{(i)})^2\\ &=\frac{1}{2}\sum_{i=1}^{n}(\mathrm{y^{(i)}-\mathrm{w}^Tx^{(i)}})^2 \end{aligned}$$于是剩下的问题就是使得这个函数能取得最小值了。
梯度下降算法
如果是对函数取最小值,我们首先想到的肯定是求取函数的极小值。——而计算机是不会自己求函数的导数的,那要怎样才能得到最小值呢?这里就需要利用计算机的自身特性(可以快速进行大量计算),与逐步逼近法类似,即寻找误差函数梯度的相反方向来对 weight 进行修改,以实现将误差函数的下降。
大致呈现下面这样的样子:
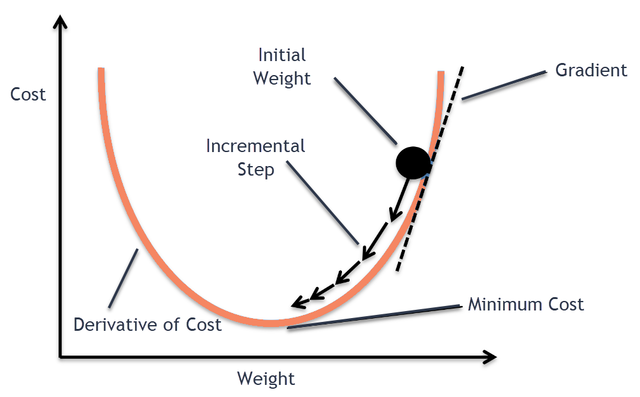
随着 weight 的不断修改,误差函数的值便会逐步逼近极值,这种方法就叫做梯度下降法,有时也叫做最速下降法 (当然如果要求取最大值那么就是梯度上升法,或者也叫做最速上升法)。常用的梯度下降算法有批量梯度下降算法、随机梯度下降算法和小批量梯度下降算法。
批量梯度下降算法 (Batch Gradient Descent, BGD)
批量梯度下降算法对所有数据都进行误差函数计算,然后不断反复的更新 weight 使得误差函数减小,直到满足要求时停止。此时的 weight 可以表达为:
$$\mathrm{w}:=\mathrm{w}-\eta\nabla{E(\mathrm{w})}$$
这里的$\eta$为学习速率。
对于$\nabla{E}(\mathrm{w})$的推导如下:
$$\begin{aligned} \nabla{E(\mathrm{w})}&=\frac{\partial}{\partial\mathrm{w}}E(\mathrm{w})\\ &=\frac{1}{2}\sum_{i=1}^{n}\frac{\partial}{\partial\mathrm{w}}(y^{(i)}-\bar{y}^{(i)})^2\\ &=\sum_{i=1}^{n} (y^{(i)}-\bar{y}^{(i)}) \cdot \frac{\partial}{\partial\mathrm{w}} (y^{(i)}-\bar{y}^{(i)})\\ &=-\sum_{i=1}^{n}(y^{(i)}-\bar{y}^{(i)})\mathrm{x} \end{aligned}$$由此则有(公式好麻烦):
$$\mathrm{w}_{new}=\mathrm{w}_{old}+\eta\sum_{i=1}^{n}(y^{(i)}-\bar{y}^{(i)})\mathrm{x}^{(i)}$$由上式我们可以得到:使用 BGD 时,每一次的参数更新都用到了所有的训练数据。因此如果训练数据非常多的话,是非常耗时的,最终会导致训练效率降低。但 BGD 的梯度下降可以保证每一次调整都是沿着最佳方向进行的。
(下面是代码实现)
import numpy as np
def BatchGradientDescent(x, y, eta, rnd):
weight = np.ones([x.shape[1]])
xTrains = x.transpose()
for i in range(rnd):
loss = y - np.dot(x, weight)
gradient = np.dot(xTrains, loss)
weight = weight + eta * gradient
return weight
def predict(x, weight):
m, n = np.shape(x)
xTest = np.ones((m, n + 1))
xTest[:, :-1] = x
res = np.dot(xTest, weight)
return res
随机梯度下降算法 (Stochastic Gradient Descent, SGD)
SGD 是利用每个样本的损失函数的梯度来更新θ,换句话说就是使用单个样本的误差来解释全部样本的误差。相比于 BGD 的全局计算,SGD 在每次更新中,只计算一个样本。这样的话只要数据集足够大,那么就可以实现和 BGD 相近的效果,而计算量会少很多。此时的 weight 可以表达为:
$$\mathrm{w}_{new}=\mathrm{w}_{old}+\eta(y^{(i)}-\bar{y}^{(i)})\mathrm{x}^{(i)}$$(下面是代码实现)
import numpy as np
def StochasticGradientDescent(x, y, eta, rnd):
weight = np.zeros([x.shape[1]])
for i in range(rnd):
for seed in range(x.shape[0]):
loss = y[seed] - np.dot(x[seed], weight)
gradient = np.dot(x[seed], loss)
weight = weight + eta * gradient
return weight
def predict(x, weight):
m, n = np.shape(x)
xTest = np.ones((m, n + 1))
xTest[:, :-1] = x
res = np.dot(xTest, weight)
return res
小批量梯度下降算法 (Min-Batch Gradient Descent, MBGD)
MBGD 使用分组的思想,将大数据集分成多个单元,再在每个单元中应用批量梯度下降算法。假设将全部数据分成$\frac{n}{m}$份,则:
$$\mathrm{w}_{new}=\mathrm{w}_{old}+\eta\cdot\frac{1}{m}\sum_{i=1}^{n}(y^{(i)}-\bar{y}^{(i)})\mathrm{x}^{(i)}$$(下面是代码实现)
import numpy as np
def MinBatchGradientDescent(x, y, eta, rnd, div):
weight = np.ones([x.shape[1]])
p = int(x.shape[0] / div)
for k in range(div):
px = x[k * p:k+1 * p]
py = y[k * p:k+1 * p]
xTrains = px.transpose()
for i in range(rnd):
loss = py - np.dot(px, weight)
gradient = np.dot(xTrains, loss)
weight = weight + eta * gradient
return weight
def predict(x, weight):
m, n = np.shape(x)
xTest = np.ones((m, n + 1))
xTest[:, :-1] = x
res = np.dot(xTest, weight)
return res