基础概念
Relu 函数
线性整流函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激励函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。标准 Relu 函数的定义是:
$$f(x)= max(0,x)$$
其导数为
$$f'(x)= \begin{cases} 1& y>0\\ 0& else \end{cases}$$它还有一些其他变种形式,如噪声线性整流函数,即在原函数的基础上加上一个正态分布的噪声:
$$f(x)= max(0,x+Y)$$
相比 Sigmoid 函数中大量的指数和对数运算,使用 Relu 函数能够使得神经网络整体计算成本下降,同时它避免了避免了梯度爆炸和梯度消失问题,能够实现更加有效率的梯度下降以及反向传播。其他研究表明,这个函数还有稀疏性的优势。
卷积
我们先从泛函分析中的卷积入手。卷积(又称叠积(convolution)、褶积或旋积),是数学分析中一种重要的运算。设: $f(x)$、$g(x)$ 是 $R$ 上的两个可积函数,作积分:
$$\int_{-\infty}^{\infty} f(\tau) g(x - \tau), \mathrm{d}\tau$$
离散化:
$$(f * g)[n]\ \ \stackrel{\mathrm{def}}{=}\ \sum_{m=-\infty}^{\infty} {f[m] g[n-m]} $$
推广到二维空间:
$$C_{s,t}=A * B=\sum_0^{m_a-1}\sum_0^{n_a-1} A_{m,n}B_{s-m,t-n}$$
这个便是二维卷积公式。
定义两个矩阵 A,B:
$$A= \begin{bmatrix} a_1&a_2&a_3 \\ a_4&a_5&a_6 \\ a_7&a_8&a_9 \\ \end{bmatrix},\qquad B= \begin{bmatrix} 1&1 \\ 0&0 \\ \end{bmatrix}$$在二维卷积的运算下结果为:
$$C_{s,t}= \begin{bmatrix} a_4+a_5&a_5+a_6 \\ a_7+a_8&a_8+a_9 \\ \end{bmatrix}$$但是机器学习范畴的卷积稍有不同,它是对应区域对应元素相乘,即互相关 (cross-correlation)。在互相关的运算下结果为:
$$C_{s,t}= \begin{bmatrix} a_1+a_2&a_2+a_3 \\ a_4+a_5&a_5+a_6 \\ \end{bmatrix}$$因此需要将卷积运算的数学表达修改为:
$$C_{s,t}=A * B=\sum_0^{m_a-1}\sum_0^{n_a-1} A_{m,n}B_{s+m,t+n}$$
网络结构
一般常见的卷积神经网络有下面的结构:
INPUT -> [[CONV]*N -> POOL?]*M -> [FC]*K
翻译成中文则为:输入层 > [ 卷积层 * N > 池化层 (可选) ] * M > 全连接层 * K
举个例子,一个典型的卷积神经网络如下图所示
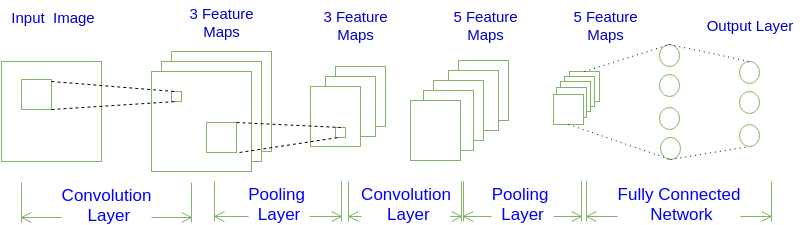
其结构则为:
INPUT -> CONV -> POOL -> CONV -> POOL -> FC -> FC
翻译成中文则为:输入层 > [ 卷积层 > 池化层 ] * 2 > 全连接层 * 2
正向传播
卷积层
前面叙述了互相关的算术表达,这里利用互相关来完成卷积层的输出。我们知道,对于一个神经元他的输出一般是:
$$ a=f(w^Tx)$$
其中 $w$ 是权重。将 $w^Tx$ 用卷积(互相关)结果替换,考虑偏置量和输入层深度以后可以写成:
$$a_{i,j}=f(\sum_{d=0}^{D-1}\sum_{m=0}^{F-1}\sum_{n=0}^{F-1}w_{d,m,n}x_{d,i+m,j+n}+w_b)$$
其中$f$是激活函数,即Relu 函数。上式改写为向量形式:
$$A=f(\sum_{d=0}^{D-1}Conv(X_d, W_d)+w_b)$$
定义两个矩阵 A、B,前者是上一层的输入数据,后者是参与运算的卷积核:
$$A= \begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3} \\ a_{2,1}&a_{2,2}&a_{2,3} \\ a_{3,1}&a_{3,2}&a_{3,3} \\ \end{bmatrix},\qquad B= \begin{bmatrix} w_{1,1}&w_{1,2} \\ w_{2,1}&w_{2,2} \\ \end{bmatrix}$$通常我们需要在参与运算的矩阵周围加上一定量的 Zero Padding 以提升边缘敏感性:
$$A= \begin{bmatrix} 0&0&0&0&0 \\ 0&a_{1,1}&a_{1,2}&a_{1,3}&0 \\ 0&a_{2,1}&a_{2,2}&a_{2,3}&0 \\ 0&a_{3,1}&a_{3,2}&a_{3,3}&0 \\ 0&0&0&0&0 \end{bmatrix}$$在确定的步长 (Stride) 下进行卷积运算,我们就可以得到卷积的输出:
$$C_n= \begin{bmatrix} u_{1,1}&u_{1,2} \\ u_{2,1}&u_{2,2} \\ \end{bmatrix}$$另外,如有特殊的 (非 1) 步长 (Stride) 或者 Padding,卷积前后矩阵的宽高服从以下运算:
$$\begin{aligned} W_2 &= (W_1 - F + 2P)/S + 1\\ H_2 &= (H_1 - F + 2P)/S + 1 \end{aligned}$$在卷积输出中加入偏置项并引入激活函数,我们就可以得到卷积层的输出:
$$C_n= \begin{bmatrix} f(u_{1,1}+bias_n)&f(u_{1,2}+bias_n) \\ f(u_{2,1}+bias_n)&f(u_{2,2}+bias_n) \\ \end{bmatrix}$$池化层
池化 (Pooling) 层主要的作用通过去掉上一层结果中不重要的样本,进一步减少参数数量。Pooling 的方法很多,常用的是 Max Pooling 和 Mean Pooling,前者是基于最大值的池化,也称为最大池化,后者是基于平均值的池化,也称为平均池化。考虑一个矩阵:
$$A= \begin{bmatrix} 8&5&0&5 \\ 9&2&8&3 \\ 6&9&3&9 \\ 8&5&7&5 \\ \end{bmatrix}$$进行范围为$2*2$最大池化后:
$$B= \begin{bmatrix} 9&8 \\ 9&9 \\ \end{bmatrix}$$进行范围为$2*2$平均池化后:
$$B= \begin{bmatrix} 6&4 \\ 7&6 \\ \end{bmatrix}$$全连接层
基于全连接神经网络进行分类判别,即:
$$\vec{a}=\sigma(W\cdot\vec{x})$$
反向传播
全连接层
详细内容可以参考上一篇文章,基于以下规则进行误差传递和梯度更新:
对于输出层:
$$\delta=y(1-y)(t-y)$$
对于隐藏层:
$$\delta^{l-1}=f'(net^{l-1})(W^{l})^T\delta^l\\ W^l \gets W^l + \eta\cdot \delta^l \cdot x^T\\ a=\sigma(W^l \cdot a^{l-1})$$卷积层
误差项
有以下定义:
$$\begin{aligned} net^l&=conv(W^l, a^{l-1})+w_b\\ a^{l}&=f^{l}(net^{l}) \end{aligned}$$其中 $net^l$ 是本层的加权输入,$a^{l}$ 是本层的输出值。因此有:
$$a^{l}=f^{l}(conv(W^l, a^{l-1})+w_b)$$
上一层的 Sensitive Map(即权重灵敏度)可以表示为:
$$\begin{aligned} \delta^{l-1}&=\frac{\partial{E_d}}{\partial{net^{l-1}}}\\ &=\frac{\partial{E_d}}{\partial{a^{l-1}}}\frac{\partial{a^{l-1}}}{\partial{net^{l-1}}}\\ &=\frac{\partial{E_d}}{\partial{a^{l-1}}}f'(net^{l-1}) \end{aligned}$$下面分析 $\frac{\partial{E_d}}{\partial{a^{l-1}}}$ 的求法。假设参与运算的矩阵和卷积核分别为:
$$A= \begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3} \\ a_{2,1}&a_{2,2}&a_{2,3} \\ a_{3,1}&a_{3,2}&a_{3,3} \\ \end{bmatrix},B= \begin{bmatrix} w_{1,1}&w_{1,2} \\ w_{2,1}&w_{2,2} \\ \end{bmatrix}$$Sensitive Map 为:
$$\delta^l= \begin{bmatrix} \delta^l_{1,1}&\delta^l_{1,2} \\ \delta^l_{2,1}&\delta^l_{2,2} \\ \end{bmatrix}$$那么对于 $a_{1,1}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{1,1}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{a^{l-1}_{1,1}}}\\ &=\delta^l_{1,1}w_{1,1} \end{aligned}$$对于 $a_{1,2}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{1,2}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{a^{l-1}_{1,2}}}+\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{a^{l-1}_{1,2}}}\\ &=\delta^l_{1,1}w_{1,2}+\delta^l_{1,2}w_{1,1} \end{aligned}$$对于 $a_{1,3}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{1,3}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{a^{l-1}_{1,3}}}\\ &=\delta^l_{1,2}w_{1,2} \end{aligned}$$对于 $a_{2,1}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{2,1}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{a^{l-1}_{2,1}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{a^{l-1}_{2,1}}}\\ &=\delta^l_{1,1}w_{2,1}+\delta^l_{2,1}w_{2,1} \end{aligned}$$对于 $a_{2,2}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{2,2}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{a^{l-1}_{2,2}}}+\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{a^{l-1}_{2,2}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{a^{l-1}_{2,2}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{a^{l-1}_{2,2}}}\\ &=\delta^l_{1,1}w_{2,2}+\delta^l_{1,2}w_{2,1}+\delta^l_{2,1}w_{1,2}+\delta^l_{2,2}w_{1,1} \end{aligned}$$对于 $a_{2,3}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{2,3}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{a^{l-1}_{2,3}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{a^{l-1}_{2,3}}}\\ &=\delta^l_{1,2}w_{2,2}+\delta^l_{2,2}w_{1,2} \end{aligned}$$对于 $a_{3,1}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{1,1}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{a^{l-1}_{3,1}}}\\ &=\delta^l_{2,1}w_{2,1} \end{aligned}$$对于 $a_{3,2}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{1,2}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{a^{l-1}_{3,2}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{a^{l-1}_{3,2}}}\\ &=\delta^l_{2,1}w_{2,2}+\delta^l_{2,2}w_{2,1} \end{aligned}$$对于 $a_{3,3}$:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{a^{l-1}_{3,3}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{a^{l-1}_{3,3}}}\\ &=\delta^l_{2,2}w_{2,2} \end{aligned}$$故 $\frac{\partial{E_d}}{\partial{a^{l-1}}}$ 的结果为:
$$\frac{\partial{E_d}}{\partial{a^{l-1}}}= \begin{bmatrix} \delta^l_{1,1}w_{1,1}&\delta^l_{1,1}w_{1,2}+\delta^l_{1,2}w_{1,1}&\delta^l_{1,2}w_{1,2} \\ \delta^l_{1,1}w_{2,1}+\delta^l_{2,1}w_{2,1}&\sum_i \sum_j \delta^l_{i,j}w_{2,2}&\delta^l_{1,2}w_{2,2}+\delta^l_{2,2}w_{1,2}\\ \delta^l_{2,1}w_{2,1}&\delta^l_{2,1}w_{2,2}+\delta^l_{2,2}w_{2,1}&\delta^l_{2,2}w_{2,2} \end{bmatrix}$$注意到这个矩阵和原矩阵 $A$ 形状相同,考虑将 Sensitive Map 和卷积核变换为:
$$\delta^l= \begin{bmatrix} 0&0&0&0\\ 0&\delta^l_{1,1}&\delta^l_{1,2}&0 \\ 0&\delta^l_{2,1}&\delta^l_{2,2}&0 \\ 0&0&0&0\\ \end{bmatrix},B= \begin{bmatrix} w_{2,2}&w_{2,1} \\ w_{1,2}&w_{1,1} \\ \end{bmatrix}$$实际上是对前者进行了 Zero Padding,对后者进行了倒置(旋转 180 度)。其中 Sensitive Map 的 Zero Padding 可以通过卷积结果的逆运算得出,即:
$$\begin{aligned} P_W &= (W_2 - 1 + F - W_1)/2 \\ P_H &= (H_2 - 1 + F - H_1)/2 \end{aligned}$$使用变换后的两个矩阵进行卷积便可以得到 $\frac{\partial{E_d}}{\partial{a^{l-1}}}$。用公式可以表示为:
$$\frac{\partial{E_d}}{\partial{a^{l-1}}}=pad(\delta^l)* rot180(W^l)$$
星号表示卷积,符号 $\circ$ 表示 element-wise product,即将矩阵中每个对应元素相乘。那么 $\delta^{l-1}$ 可以表示为:
$$\delta^{l-1}=pad(\delta^l)* rot180(W^l)\circ f'(net^{l-1})$$
如果 Filter 层数为$D$,则需要将各层 Filter 分别进行卷积,最后相加得到$delta$:
$$\delta^{l-1}=\sum_{d=0}^D pad(\delta_d^l)*rot180(W_d^l)\circ f'(net^{l-1})$$如果输入层数为$N$,则需要将每一层对应的 Filter 进行独立计算(如有多层 Filter 则需要求和),得到每一个输入层的$delta$:
$$\delta^{l-1}_n=\sum_{d=0}^D pad(\delta_d^l)*rot180(W_d^l)\circ f'(net^{l-1})$$如果卷积步长为 S 时,可以先观察一下卷积结果的特征。对于以下矩阵和卷积核:
$$A=\begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4} \\ a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4} \\ a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \\ a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4} \\ \end{bmatrix},B= \begin{bmatrix} w_{1,1}&w_{1,2} \\ w_{2,1}&w_{2,2} \\ \end{bmatrix}$$当步长为 1(Stride=1) 时,有:
$$Conv(A,B)=\begin{bmatrix} b_{1,1}&b_{1,2}&b_{1,3} \\ b_{2,1}&b_{2,2}&b_{2,3} \\ b_{3,1}&b_{3,2}&b_{3,3} \\ \end{bmatrix}$$而对于步长为 2(Stride=2) 时,有:
$$Conv(A,B)=\begin{bmatrix} c_{1,1}&c_{1,2}\\ c_{2,1}&c_{2,2}\\ \end{bmatrix}$$观察计算过程可以发现,大于 1 步长所产生的结果矩阵其实相当于从步长为 1 的结果矩阵中选取了特定点组合而成。由于 Sensitive Map 的形状和卷积结果的形状是相同的,而我们需要将 Sensitive Map 与 w 相卷积以得到输入层的 $\delta$,所以需要先将 Sensitive Map 填充为卷积步长为 1 时应有样子(填充 0),再按照原来的方法进行计算,即:
$$\begin{bmatrix} c_{1,1}&c_{1,2}\\ c_{2,1}&c_{2,2}\\ \end{bmatrix}\to\begin{bmatrix} c_{1,1}&0&c_{1,2}\\ 0&0&0\\ c_{2,1}&0&c_{2,2}\\ \end{bmatrix}$$可以先通过以下公式计算步长为 1 时 Feature Map 的宽和高:
$$\begin{aligned} W_2 &= (W_1 - F + 2P)/S + 1\\ H_2 &= (H_1 - F + 2P)/S + 1 \end{aligned}$$其中 F 指 Fliter 的宽或高,P 为本层的 Zero Padding,S 是步辐。使用这个宽高创建以 0 填充的矩阵:将小的卷积结果数据按照以下位置进行映射:
$$[i, j] \to [(i-1) * stride, (j-1)*stride] $$
其中$stride$是前向计算卷积时的步长。
权重梯度
考虑以下输入和 Filter:
$$A= \begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3} \\ a_{2,1}&a_{2,2}&a_{2,3} \\ a_{3,1}&a_{3,2}&a_{3,3} \\ \end{bmatrix},B= \begin{bmatrix} w_{1,1}&w_{1,2} \\ w_{2,1}&w_{2,2} \\ \end{bmatrix}$$Sensitive Map 为:
$$\delta^l= \begin{bmatrix} \delta^l_{1,1}&\delta^l_{1,2} \\ \delta^l_{2,1}&\delta^l_{2,2} \\ \end{bmatrix}$$我们可以发现,对于每个权重项 $w_{i,j}$,都会对结果的所有项产生影响:
$$net^j=W*patch(A)+w_b$$
那么如果要求 $w$ 的误差贡献,可以对每个 patch 求偏导数:
$$\frac{\partial{E_d}}{\partial{w_{i,j}}}=\sum_{x\in patch} \frac{\partial{E_d}}{\partial{net^{l}_x}}\frac{\partial{net^{l}_x}}{\partial{w_{i,j}}}$$对于$\frac{\partial{E_d}}{\partial{w_{1,1}}}$:
$$\frac{\partial{E_d}}{\partial{w_{1,1}}}=\delta^l_{1,1}a^{l-1}_{1,1}+\delta^l_{1,2}a^{l-1}_{1,2}+\delta^l_{2,1}a^{l-1}_{2,1}+\delta^l_{2,2}a^{l-1}_{2,2}$$对于$\frac{\partial{E_d}}{\partial{w_{1,2}}}$:
$$\frac{\partial{E_d}}{\partial{w_{1,2}}}=\delta^l_{1,1}a^{l-1}_{1,2}+\delta^l_{1,2}a^{l-1}_{1,3}+\delta^l_{2,1}a^{l-1}_{2,2}+\delta^l_{2,2}a^{l-1}_{2,3}$$我们发现,其实这个权重梯度可以看作是输入层和 Sensitive Map 在做卷积。即:
$$\frac{\partial{E_d}}{\partial{w}}=Conv(\delta^l, a^{l-1})$$
其中 $\delta^l$ 是本层的的 Sensitivity Map,$a^{l-1}$ 是本层的输入,即上一层的输出。
对于偏置项运用同样的计算方法,有:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{w_b}}&=\frac{\partial{E_d}}{\partial{net_b}}\frac{\partial{net_b}}{\partial{w_b}}\\ &=\sum\delta^l \end{aligned}$$即对本层的 Sensitivity Map 求和
池化层
池化层没有权重,因此也没有权重梯度,只需计算 $\delta$ 的传递即可。
采用 Max Pooling 时,有:
$$\begin{aligned} \delta^{l-1}_{max}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{max}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{max}}}\frac{\partial{net^{l}_{max}}}{\partial{net^{l-1}_{max}}}\\ &=\delta^{l}_{max}\\ \end{aligned}$$$$\delta^{l-1}_{others}=0$$
即对于 Max Pooling,下一层的 $\delta$ 仅会传递到上一层对应区块中的最大值节点,而其他节点的 $\delta$ 都是 0。
采用 Mean Pooling 时,有:
$$\begin{aligned} \delta^{l-1}_n&=\frac{\partial{E_d}}{\partial{net^{l-1}_n}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_n}}\frac{\partial{net^{l}_n}}{\partial{net^{l-1}_n}}\\ &=\frac{1}{4}\delta^{l}_n\\ \end{aligned}$$即对于 Mean Pooling,下一层的$\delta$会平均分配到上一层对应区块中的所有节点。上面这个算法可以使用克罗内克积 (Kronecker product) 来表示,即:
$$\delta^{l-1} = \delta^l\otimes(\frac{1}{n^2})_{n\times n}$$
举个例子,假设池化区域大小为 $[2,2]$,本层 $\delta^{l}$ 为:
$$\delta^{l}= \begin{bmatrix} 0.6&0.4 \\ 0.7&0.6 \\ \end{bmatrix}$$先按照输入矩阵生成区域:
$$\delta^{l}= \begin{bmatrix} 0&0&0&0 \\ 0&0.6&0.4&0 \\ 0&0.7&0.6&0 \\ 0&0&0&0 \end{bmatrix}$$然后将原始矩阵中的最大值点进行映射:
$$\delta^{l}= \begin{bmatrix} 0.6&0&0&0.4 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0.7&0&0.6 \end{bmatrix}$$对于平均池化,有:
$$\delta^{l}= \begin{bmatrix} 0.15&0.15&0.1&0.1 \\ 0.15&0.15&0.1&0.1 \\ 0.175&0.175&0.15&0.15 \\ 0.175&0.175&0.15&0.15 \end{bmatrix}$$实现
这个脚本写到一半枯了 qwq,不过基本的各个网络层的实现已经完成,只剩下连接层和总网络类了。
主要需要注意的是,在全连接层和池化层之间的维度转换。因为全连接层是一维的,而无论是卷积层还是池化层都是二维以上的,因此交界处无论是$\delta$还是$a$都要进行维度转换,同时需要保持位置一致。
import os
import struct
import numpy as np
class FullConnectLayer:
def __init__(self, _in, _out):
self.out = _out
self.front = lambda x: 1 / (1 + np.exp(-x))
self.back = lambda y: y * (1 - y)
self.weight = np.random.uniform(-0.5, 0.5, (_out, _in))
self.array = None
self.delta = None
self.grad = None
def forward(self, array):
self.array = array
return self.front(np.dot(self.weight, array))
def propagation(self, delta):
return self.back(self.array) * np.dot(np.transpose(self.weight), delta)
def gradient(self):
self.grad = np.dot(self.delta, np.transpose(self.array))
def update(self, rate):
self.weight += rate * self.grad
class Filter:
def __init__(self, depth, height, width):
self.weights = np.random.uniform(-0.1, 0.1, (depth, height, width))
self.bias = 0
self.weights_grad = np.zeros([depth, height, width])
self.bias_grad = 0
def update(self, _rate):
self.weights -= _rate * self.weights_grad
self.bias -= _rate * self.bias_grad
class ConvolutionLayer:
def __init__(self, _input, _filter, _padding, _stride, _rate):
# Input Variables
self.ic, self.ih, self.iw = _input
self.fc, self.fh, self.fw = _filter
self.padding, self.stride, self.rate = _padding, _stride, _rate
# Initialize
self.oh, self.ow = self.fmh(self.ih, self.fh), self.fmh(self.iw, self.fw)
self.filter = [Filter(self.ic, self.fh, self.fw) for _ in range(self.fc)]
self.output = np.zeros([self.fc, self.oh, self.ow])
self.array = None
self.delta = None
self.padded = None
# Functions
self.activator = lambda x: np.max(0, x)
self.back = lambda x: 1 if x > 0 else 0
self.pad = lambda a, p: np.array(list(map(lambda x: np.pad(x, p, mode='constant'), a)))
self.fmh = lambda x, f: (x - f + 2 * self.padding) / self.stride + 1
self.bmh = lambda x, f: (x - f + 2 * self.padding) + 1
self.zph = lambda x, f, p: (x + f - 1 - p) / 2
self.flip = lambda x: np.array(list(map(lambda i: np.rot90(i, 2), x)))
self.std = lambda x: x.reshape(1, x.shape[0], x.shape[1]) if len(x.shape) == 2 else x
def forward(self, array):
self.array = self.std(array)
self.padded = self.pad(self.array, self.padding)
for k in range(self.fc):
_filter = self.filter[k]
self.output[k] = self.convolution(_filter.weights, _filter.bias, self.padded, self.stride)
self.operation(self.output, self.activator)
def convolution(self, weights, bias, array, stride):
# TransForm
weights = self.std(weights)
array = self.std(array)
_dep, _fh, _fw = weights.shape
_dep, _ih, _iw = array.shape
_oh, _ow = self.fmh(_ih, _fh), self.fmh(_iw, _fw)
result = np.array([_oh, _ow])
for i in range(_oh):
for j in range(_ow):
start_i, start_j = i * stride, j * stride
run = array[:, start_i: start_i + _fh, start_j: start_j + _fw]
result[i, j] = np.sum(run * weights) + bias
return result
def propagation(self, array, backward):
array = self.std(array)
standard = self.expend(array)
full = self.pad(standard, self.zph(self.ih, self.fh, standard.shape[2]))
_delta = np.zeros((self.ic, self.ih, self.iw))
for k in range(self.fc):
flipped_weights = self.flip(self.filter[k].weights)
delta = np.zeros((self.ic, self.ih, self.iw))
for s in range(self.ic):
delta[s] = self.convolution(flipped_weights[k], 0, full[s], 1)
_delta += delta
_delta *= self.operation(self.array, backward)
return _delta
def expend(self, array):
array = self.std(array)
_dep, _ih, _iw = array.shape
_oh, _ow = self.bmh(self.ih, self.fh), self.bmh(self.iw, self.fw)
expanded = np.zeros((_dep, _oh, _ow))
for i in range(_ih):
for j in range(_iw):
i_pos = i * self.stride
j_pos = j * self.stride
expanded[:, i_pos, j_pos] = array[:, i, j]
return expanded
def gradient(self, array):
array = self.std(array)
for f in range(self.fc):
_filter = self.filter[f]
for d in range(_filter.weights.shape[0]):
_filter.weights_grad[d] = self.convolution(array, 0, self.padded[d], self.stride)
_filter.bias_grad = np.sum(array)
def update(self):
[_filter.update(self.rate) for _filter in self.filter]
@staticmethod
def operation(array, operation):
for i in np.nditer(array, op_flags=['readwrite']):
i[...] = operation(i)
class PoolingLayer:
def __init__(self, _input, _filter, _stride):
self.ic, self.ih, self.iw = _input
self.fh, self.fw = _filter
self.stride = _stride
self.oh = (self.ih - self.fh) / self.stride + 1
self.ow = (self.iw - self.fw) / self.stride + 1
self.output = np.zeros((self.ic, self.oh, self.ow))
self.delta = None
self.std = lambda x: x.reshape(1, x.shape[0], x.shape[1]) if len(x.shape) == 2 else x
def forward(self, _array):
_array = self.std(_array)
for d in range(self.ic):
for i in range(self.oh):
for j in range(self.ow):
start_i, start_j = i * self.stride, j * self.stride
patch = _array[d, start_i: start_i + self.fh, start_j: start_j + self.fw]
self.output[d, i, j] = np.max(patch)
def backward(self, _input, _array) -> np.array:
_array = self.std(_input)
self.delta = np.zeros_like(_input)
for d in range(self.ic):
for i in range(self.oh):
for j in range(self.ow):
start_i, start_j = i * self.stride, j * self.stride
patch = _input[d, start_i: start_i + self.fh, start_j: start_j + self.fw]
for _i in range(self.fh):
for _j in range(self.fw):
if patch[_i, _j] == np.max(patch):
self.delta[d, start_i + _i, start_j + _j] = _array[d, i, j]
def load(path, kind):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path, '%s-labels-idx1-ubyte' % kind)
images_path = os.path.join(path, '%s-images-idx3-ubyte' % kind)
with open(labels_path, 'rb') as path:
_, _ = struct.unpack('>II', path.read(8))
labels = np.fromfile(path, dtype=np.uint8)
with open(images_path, 'rb') as path:
_, _, _, _ = struct.unpack('>IIII', path.read(16))
images = np.fromfile(path, dtype=np.uint8).reshape(len(labels), 784)
return (images / 2550), labels
class ConnectionLayer:
def __init__(self):
pass
class Network:
def __init__(self):
"""
Simulate LeNet-5:
input(32*32) -> 6 * [28*28]
"""
self.layer = [
ConvolutionLayer((1, 32, 32), (6, 7, 7), 1, 1, 0.1),
PoolingLayer((6, 28, 28), (2, 2), 1),
ConvolutionLayer((6, 14, 14), (16, 9, 9), 2, 1, 0.05),
PoolingLayer((16, 10, 10), (2, 2), 1),
ConnectionLayer(),
FullConnectLayer(120, 84),
FullConnectLayer(84, 10)
]
def evaluate(network, test_data_set, test_labels):
error = 0.0
total = len(test_data_set)
data = np.column_stack((test_data_set, np.ones([test_data_set.shape[0], 1])))
for i in range(total):
test = data[i].reshape([data[i].shape[0], 1])
prt = network.predict(test)
if test_labels[i] != int(np.where(prt == np.max(prt))[0]):
error += 1
return round(float(error) / float(total) * 100, 2)
def main():
train_images, train_labels = load('.', 'train')
test_images, test_labels = load('.', 't10k')
pass
if __name__ == "__main__":
try:
main()
except KeyboardInterrupt:
pass