Sigmoid 函数
Sigmoid 函数是一类形状像 S 字母的函数,称为 S 型生长曲线。常见的 S 函数包括逻辑函数、双曲正弦函数、反正切函数、古德曼函数和平滑阶跃函数等。
我们先从机器学习中较为常见的 Logistic 函数入手,其定义为:
$$sigmoid(x)=\frac{1}{1+e^{-x}}$$
其函数图像如下:

这个函数有一个特性,即其导数是原函数的函数:
$$\begin{aligned} &y=sigmoid(x)\\ &y'=y(1-y) \end{aligned}$$因此其导数可以通过本身来进行计算。下文使用 Sigmoid 函数作为激活函数构建神经网络,并实现反向传播算法。
神经网络
将感知器或者线性单元所使用的激活函数稍作拓展,当使用 Sigmoid 函数最为激活函数时,神经元结构如下图所示:
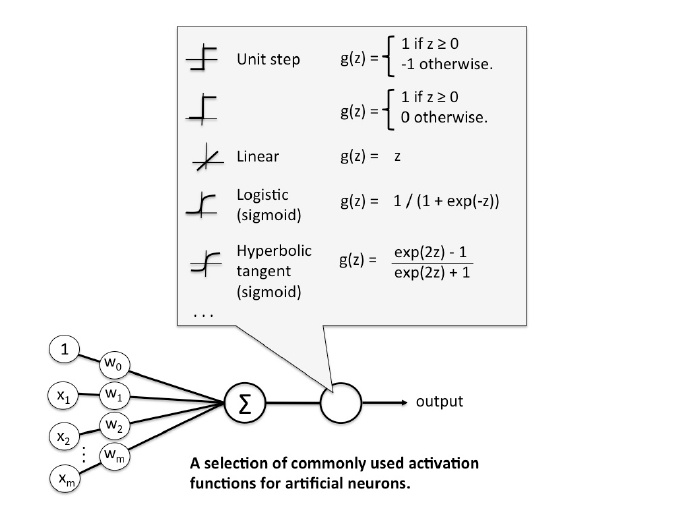
多个上图的神经元相互连接构成的网络结构叫做神经网络,如下图:
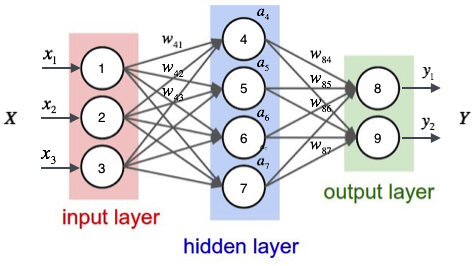
上图是一个全连接神经网络(Full Connent, FC),其组成包括:
- 输入层(input layer)数据由此层输入,其输出值为下游节点的输入值。
- 隐藏层(hidden layer)即外部不可见层,包含指定个节点个数,可以理解为神经网络的内部逻辑。
- 输出层(output layer)结果由此层输出,其每一个节点连接着上一个隐藏层的所有节点。
对于隐藏层,每个神经元都会进行以下操作:
$$a_4=f(\vec{w}^T\cdot\vec{x})$$
即使用激活函数对加权输入进行激活判定。
假设选取隐藏层的节点 4 进行观察,那么其计算结果便为:
$$\begin{aligned} a_4&=sigmoid(\vec{w}^T\cdot\vec{x})\\ &=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b}) \end{aligned}$$上式的 $w_{4b}$ 是节点 4 的偏置项,而 $w_{41},w_{42},w_{43}$ 分别为节点 1、2、3 到节点 4 连接的权重。进而我们可以得到隐藏层 4 个节点的计算结果:
$$a_4=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b})\\ a_5=sigmoid(w_{51}x_1+w_{52}x_2+w_{53}x_3+w_{5b})\\ a_6=sigmoid(w_{61}x_1+w_{62}x_2+w_{63}x_3+w_{6b})\\ a_7=sigmoid(w_{71}x_1+w_{72}x_2+w_{73}x_3+w_{7b})$$令:
$$W= \begin{bmatrix} \vec{w}_4 \\ \vec{w}_5 \\ \vec{w}_6 \\ \vec{w}_7 \\ \end{bmatrix}= \begin{bmatrix} w_{41},w_{42},w_{43},w_{4b} \\ w_{51},w_{52},w_{53},w_{5b} \\ w_{61},w_{62},w_{63},w_{6b} \\ w_{71},w_{72},w_{73},w_{7b} \\ \end{bmatrix} $$由此有:
$$\vec{a}=f(W\cdot\vec{x})\qquad $$
扩展到各层,如在开始的神经网络中,节点服从如下的计算:
$$\vec{a}_1=f(W_1\cdot\vec{x})$$
$$\vec{y}=f(W_2\cdot\vec{a}_1)$$
其中 $\vec{y}$ 是输出层的结果矩阵。
现在,我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型,那么这些权值就是模型的参数,也就是模型要学习的东西。然而,一个神经网络的连接方式、网络的层数、每层的节点数这些参数,则不是学习出来的,而是人为事先设置的。对于这些人为设置的参数,我们称之为超参数 (Hyper-Parameters)。
反向传播算法 (Backpropagation, BP)
BP 算法是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。 反向传播要求有对每个输入值期望得到的已知输出,来计算损失函数的梯度。仿照线性回归中的误差函数,我们使用误差平方和作为误差函数,然后使用随机梯度下降算法对权重进行计算:
$$E_d\equiv\frac{1}{2}\sum_{i}(t_i-y_i)^2$$
$$w_{ji}\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}$$
设 $net_j$ 是节点 $j$ 的加权输入,即:
$$net_j=\sum_{i}{w_{ji}}x_{ji}=\vec{w_j}\cdot\vec{x_j}$$
求导可得:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{w_{ji}}}&=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{net_j}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{\sum_{i}{w_{ji}}x_{ji}}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{net_j}}x_{ji} \end{aligned}$$上式中,是 $x_{ji}$ 节点 $i$ 传递给节点 $j$ 的输入值,也就是节点$i$的输出值。 对于 $\frac{\partial{E_d}}{\partial{net_j}}$,需要分为输出层和隐藏层来讨论。
对于输出层,由于 $y(j)=f(net_j)$,其中 $f$ 为激活函数,所以使用 $y_j$ 对 $\frac{\partial{E_d}}{\partial{net_j}}$ 进行变换:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{net_j}}&=\frac{\partial{E_d}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{net_j}}\\ &=\frac{\partial}{\partial{y_j}}\frac{1}{2}\sum_{i}(t_i-y_i)^2\cdot\frac{\partial f(net_j)}{\partial{net_j}}\\ &=\frac{\partial}{\partial{y_j}}\frac{1}{2}(t_j-y_j)^2\cdot y_j(1-y_j)\\ &=-(t_j-y_j)y_j(1-y_j)\\ \end{aligned}$$令 $$\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$$ 则有:
$$\begin{aligned} &\delta_j=(t_j-y_j)y_j(1-y_j) \qquad (1)\\ &w_{ji}:=w_{ji}+\eta\cdot\delta_j\cdot x_{ji} \qquad (2) \end{aligned}$$对于隐藏层,由于 $f(net_j)*w_k = net_k$,其中 $net_k$ 是下一层节点 $k \in NextLayer(j)$ 的加权输入,所以使用 $net_k$ 对 $\frac{\partial{E_d}}{\partial{net_j}}$ 进行变换:
$$\begin{aligned} \frac{\partial{E_d}}{\partial{net_j}}&=\sum_{k}\frac{\partial{E_d}}{\partial{net_k}}\frac{\partial{net_k}}{\partial{net_j}}\\ &=\sum_{k}-\delta_k\frac{\partial{net_k}}{\partial{a_j}}\frac{\partial{a_j}}{\partial{net_j}}\\ &=\sum_{k}-\delta_kw_{kj}\cdot \frac{\partial{f(net_j)}}{\partial{net_j}}\\ &=\sum_{k}-\delta_kw_{kj}\cdot a_j(1-a_j)\\ \end{aligned}$$将 $\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$ 带入上式得到:
$$\delta_j=a_j(1-a_j)\sum_{k}\delta_kw_{kj} \qquad (3)$$
对于输出层节点应用式 $(1)$,对于隐藏层节点应用式 $(3)$,并将结果在式 $(2)$ 中更新权重,循环以上步骤即可实现基于反向传播算法的神经网络训练。
向量化及实现
将式 $(1)$、式 $(2)$ 和式 $(3)$ 改写为向量形式有:
$$\vec{\delta}=\vec{y}(1-\vec{y})(\vec{t}-\vec{y})\\ \vec{\delta^{(l)}}=\vec{a}^{(l)}(1-\vec{a}^{(l)})W^T\delta^{(l+1)}\\ W \gets W + \eta\cdot \vec{\delta}\cdot\vec{x}^T\\ \vec{a}=\sigma(W\cdot\vec{x})$$其中,$\delta^{(l+1)}$ 表示第 $(l+1)$ 层的误差项。
代码实现如下(使用MINST 数据集, Python3.8):
import os
import time
import struct
import numpy as np
class Layer:
def __init__(self, _in, _out):
self.out = _out
self.front = lambda x: 1 / (1 + np.exp(-x))
self.back = lambda y: y * (1 - y)
self.weight = np.random.uniform(-0.5, 0.5, (_out, _in))
self.array = None
def forward(self, array):
self.array = array
return self.front(np.dot(self.weight, array))
def update(self, delta, rate):
dp = self.back(self.array) * np.dot(np.transpose(self.weight), delta)
self.weight += rate * np.dot(delta, np.transpose(self.array))
return dp
class Network:
def __init__(self, node):
self.layers = []
self.back = lambda y: y * (1 - y)
for k in range(len(node) - 1):
self.layers.append(Layer(node[k], node[k + 1]))
def predict(self, array):
result = array.copy()
for layer in self.layers:
result = layer.forward(result)
return result
def train(self, sample, label, epoch, rate):
"""
sample: [m, n] (no bias layer)
label: [n]
"""
# Add Bias
_input = np.column_stack((sample, np.ones([sample.shape[0], 1])))
# Generate Layers
count, p = _input.shape
# Start Training
for i in range(epoch):
for j in range(count):
result = self.predict(_input[j].reshape([p, 1]))
delta = self.back(result) * self.delta(label[j], result)
for layer in self.layers[::-1]:
delta = layer.update(delta, rate)
@staticmethod
def delta(label, predict):
ans = np.zeros([10, 1])
ans[label, 0] = 1
return ans - predict
def load(path, kind):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path, '%s-labels-idx1-ubyte' % kind)
images_path = os.path.join(path, '%s-images-idx3-ubyte' % kind)
with open(labels_path, 'rb') as path:
_, _ = struct.unpack('>II', path.read(8))
labels = np.fromfile(path, dtype=np.uint8)
with open(images_path, 'rb') as path:
_, _, _, _ = struct.unpack('>IIII', path.read(16))
images = np.fromfile(path, dtype=np.uint8).reshape(len(labels), 784)
return (images / 2550), labels
def evaluate(network, test_data_set, test_labels):
error = 0
total = len(test_data_set)
data = np.column_stack((test_data_set, np.ones([test_data_set.shape[0], 1])))
for i in range(total):
test = data[i].reshape([data[i].shape[0], 1])
prt = network.predict(test)
if test_labels[i] != int(np.where(prt == np.max(prt))[0]):
error += 1
return round(float(error) / float(total) * 100, 2)
def main():
train_images, train_labels = load('.', 'train')
test_images, test_labels = load('.', 't10k')
bp = Network([785, 100, 10])
for i in range(40):
now = time.time()
rate = 0.8 / (i + 1)
bp.train(train_images, train_labels, 1, rate)
debug = [
'Rnd: {}'.format(i),
'Err: {}%'.format(evaluate(bp, test_images, test_labels)),
'Time: {}s'.format(round(time.time() - now, 2))
]
print(' '.join(debug))
pass
if __name__ == "__main__":
try:
main()
except KeyboardInterrupt:
pass
运行结果:
kyaru# python3 c.py
Rnd: 0 Err: 9.13% Time: 15.49s
Rnd: 1 Err: 6.72% Time: 14.94s
Rnd: 2 Err: 6.07% Time: 15.43s
Rnd: 3 Err: 5.45% Time: 15.27s
Rnd: 4 Err: 5.16% Time: 14.71s
Rnd: 5 Err: 4.97% Time: 15.55s
Rnd: 6 Err: 4.76% Time: 15.39s
Rnd: 7 Err: 4.61% Time: 14.8s
Rnd: 8 Err: 4.46% Time: 15.0s
Rnd: 9 Err: 4.44% Time: 15.75s
Rnd: 10 Err: 4.3% Time: 16.0s
Rnd: 11 Err: 4.23% Time: 15.67s
Rnd: 12 Err: 4.19% Time: 15.46s
Rnd: 13 Err: 4.14% Time: 14.9s
Rnd: 14 Err: 4.06% Time: 15.35s
Rnd: 15 Err: 4.03% Time: 15.63s
Rnd: 16 Err: 3.99% Time: 15.95s
Rnd: 17 Err: 3.95% Time: 15.34s
Rnd: 18 Err: 3.96% Time: 15.65s
Rnd: 19 Err: 3.93% Time: 15.68s
Rnd: 20 Err: 3.86% Time: 15.33s
Rnd: 21 Err: 3.82% Time: 15.78s
Rnd: 22 Err: 3.81% Time: 15.57s
Rnd: 23 Err: 3.76% Time: 15.54s
Rnd: 24 Err: 3.74% Time: 15.79s
Rnd: 24 Err: 3.74% Time: 15.79s
Rnd: 25 Err: 3.74% Time: 15.87s
Rnd: 26 Err: 3.73% Time: 15.23s
Rnd: 27 Err: 3.71% Time: 15.18s
Rnd: 28 Err: 3.7% Time: 15.93s
Rnd: 29 Err: 3.7% Time: 15.51s
Rnd: 30 Err: 3.7% Time: 15.4s
Rnd: 31 Err: 3.7% Time: 15.41s
Rnd: 32 Err: 3.68% Time: 14.83s
Rnd: 33 Err: 3.66% Time: 15.38s
Rnd: 34 Err: 3.65% Time: 15.05s
Rnd: 35 Err: 3.66% Time: 14.95s
Rnd: 36 Err: 3.66% Time: 15.43s
Rnd: 37 Err: 3.64% Time: 15.2s
Rnd: 38 Err: 3.63% Time: 15.76s
Rnd: 39 Err: 3.63% Time: 15.8s
...
Rnd: 128 Err: 3.18% Time: 14.58s
Rnd: 129 Err: 3.17% Time: 14.35s
Rnd: 130 Err: 3.17% Time: 14.47s
Rnd: 131 Err: 3.17% Time: 14.11s
Rnd: 132 Err: 3.17% Time: 13.81s
Rnd: 133 Err: 3.17% Time: 13.51s
Rnd: 134 Err: 3.17% Time: 13.63s
Rnd: 135 Err: 3.16% Time: 13.71s
Rnd: 136 Err: 3.16% Time: 13.53s
Rnd: 137 Err: 3.16% Time: 13.4s
Rnd: 138 Err: 3.16% Time: 13.26s
Rnd: 139 Err: 3.16% Time: 13.46s
Rnd: 140 Err: 3.15% Time: 13.58s
Rnd: 141 Err: 3.17% Time: 13.53s
Rnd: 142 Err: 3.17% Time: 13.8s
Rnd: 143 Err: 3.16% Time: 13.26s
Rnd: 144 Err: 3.16% Time: 13.35s
Rnd: 145 Err: 3.16% Time: 13.85s
Rnd: 146 Err: 3.16% Time: 13.98s
Rnd: 147 Err: 3.16% Time: 13.98s
Rnd: 148 Err: 3.16% Time: 14.14s
Rnd: 149 Err: 3.16% Time: 14.2s
kyaru#